Sifat-sifat logaritma dan contohnya

Sifat - Sifat Logaritma

Ada 7 sifat pada logaritma ini yang akan membantu kamu dalam memecahkan masalah yang berkaitan dengan logaritma, yaitu :

Sifat 1
^alog x + ^alog y = ^alog xy
Contoh :
Sederhanakanlah !
a. ²log 4 + ²log 8
b. ³log (1/9) + ³log 81
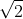
c. ²log 2 + ²log 4
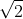
Jawab :
a. ²log 4 + ²log 8 = ²log 4 . 8 = ²log 32 = 5
b. ³log (1/9) + ³log 81= ³log (1/9). 81 = ³log 9 = 2
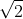
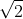
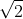
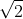
c. ²log 2 + ²log 4 = ²log 2 .4 = ²log 16 = 4

Sifat 2
^alog x – ^alog y = ^alog (x/y)
Contoh:
Sederhanakanlah!
a. ²log 16 – ² log 8
b. log 1.000 – log 100
c. ³log 18 – ³log 6
Jawab :
a. ²log 16 – ² log 8 = ²log (16/8) = ²log 2 = 1
b. log 1.000 – log 100 = log (1000/100) = log 10 = 1
c. ³log 18 – ³log 6 = ³log (18/6) = ³log 3 = 1

Sifat 3
^alog xⁿ = n . ^alog x
Contoh :
Sederhanakan!
a. 2 log 3 + 4 log 3
b. 2 log a + 2 log b
Jawab:
a. 2 log 3 + 4 log 3 = log 3² + log 3⁴
= log 9 + log 81
= log 9 . 81
= log 729

b. 2 log a + 2 log b = log a² + log b²
= log a² . b²
= log (ab)²

Ingat : 1. log 2x = log x . log x = (log x)2 log x2 = 2 log x Jadi log 2x ≠ log x2 2. Log -1x = (1/log x) Log x-1 = log (1/x) = -log x Jadi log -1x ≠ log x-1

Sifat 4
^alog b x ^blog c = ^alog c
Contoh :
a. ³log 7 x ⁷log 81 = ³log 81 = ³log 3⁴ = 4
b. ²log 5 x ⁵log 32 = ²log 32 = ²log 2⁵ = 5

Sifat 5

Contoh :
³log 7 x ⁷log 81
Jawab :




Sifat 6
a ^{alog x} = x
Contoh :
a. 5^{5log 8}
b. 4^{2log 3}
c. 9^{3log 4}
Jawab :
a. 5^{5log 8} = 8
b. 4^{2log 3} = 2^{2.2log 3} = 2^{2log 32} = 9
c. 9^{3log 4} = 3^{2.3log 4} = 3^{3log 42} = 16

Sifat 7
^anlog b^m = (n/m)^alog b
Untuk a dan b bilangan real positif, dan a ≠ 1

Contoh :
Hitunglah !
1. ⁴log 32
2. ⁸log 64
3. Jika ³log 5 = a hitunglah ²⁵log 27
Jawab :
1. ⁴log 32 = ²²log 2⁵= 5/2
2. ¹⁶log 64 = ²⁴log 2⁶= 6/4 = 3/2
3. ²⁵log 27 = ⁵²log 3³= (3/2)⁵log 3 = 3/2a